数理情報学研究室では,様々な事象に関する情報に対して数理的手法を用いることで研究を行っています.我々の研究対象は多岐にわたっており,
- 分子・細胞(例:酵素の活性,神経細胞の軸索伸長)
- 組織・器官(例:手指や舌を司る筋群,てんかん患者やクモ膜下出血患者の脳活動)
- 動物の行動(例:マウスの行動やジュウシマツの歌)
- ヒトの行動(例:絵画鑑賞,運転行動など)
- 社会(例:社会的ネットワーク内のグループ構造)
- 自然環境(例:風況予測)
- 数理的手法自体
などが挙げられます.形がなく目に見えないものもあれば,形あるものでもスケールが非常に小さいものから大きなものまであり,幅広く取り扱っていることが分かって頂けると思います.このような多様なテーマも数理情報学研究室の特徴の一つですし,それを実現可能にしているのが数理的手法だと言えます.これらの研究内容の全てを詳しくご紹介するのは難しいので,ここではそのうちの幾つかの内容に絞ってご紹介します.

神経細胞ネットワークモデルを用いたてんかんの病態
および冷却療法効果のシミュレーション研究
てんかんは近年社会的にも注目されるようになりましたが,てんかんの治療のために外科的手術が必要になることもあるとご存知でしたでしょうか?薬による治療では十分な発作抑制効果を得られない場合にそのような外科的手術が必要になるのですが,より体へのダメージを伴わないような治療の方がやはり望ましいと考えられます.そのようなダメージの少ない新たな治療法の候補として,局所脳冷却療法が挙げられます.局所脳冷却療法は,頭蓋内に冷却用の素子を埋め込み,発作時にその発生源を冷却することで発作抑制を図る治療法です.数理情報学研究室ではHodgkin-Huxley型神経細胞ネットワークのモデルを用いて,この局所冷却療法の効果をシミュレートする研究を行っています.冷却によって神経細胞の過剰な同期を元の状態に戻すことは可能なのか,その時何℃まで脳を冷却すべきなのか,どのような指標を用いれば発作の予測をより高精度に行うことができるのか,などの問題についてシミュレーションによって有益な知見を得たいと考えています.
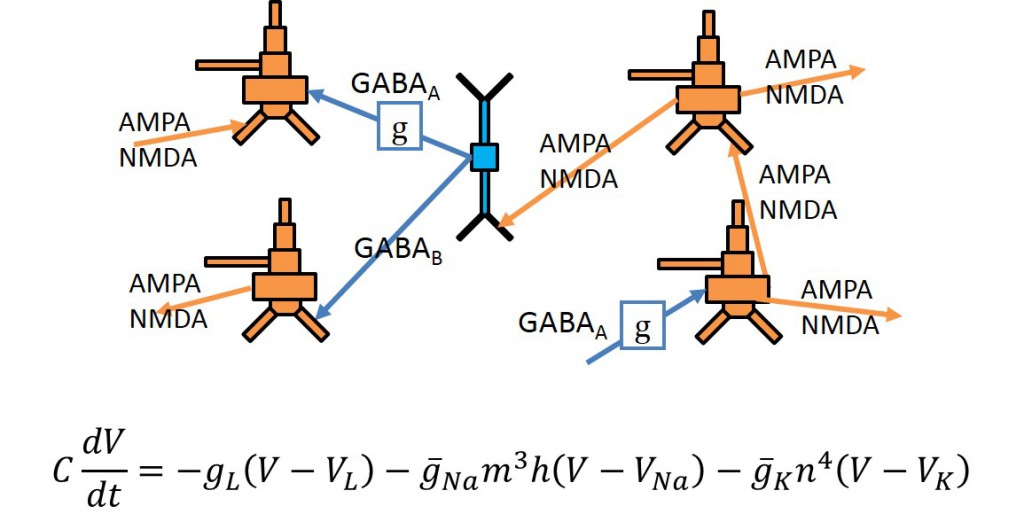
数式は個々の細胞の電気的活動を表したもの.
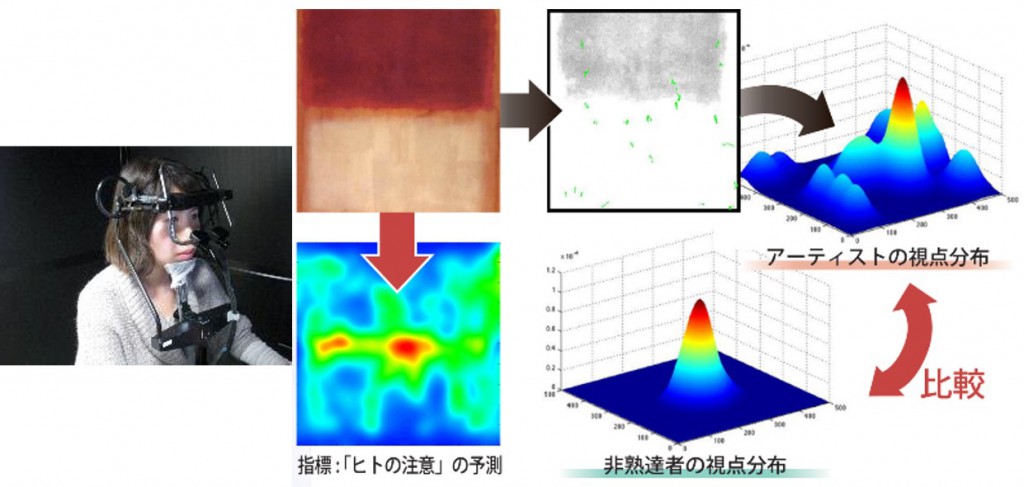
抽象画鑑賞時に画家が着目する特徴の特定
絵画,特に抽象画を鑑賞する時,一般の人にとっては着目すべきポイントがどこだか分からないこともしばしばでしょう.しかし,画家にとってはそのような着目すべきポイントが明白であるとされています.それが本当だとしたら,そしてそのポイントの特徴を知ることができれば,芸術的な素養がない人もそのような特徴を意識して見るよう訓練を受けることができるかもしれません.ところが,実際にそのようなポイントの特徴を明らかにしたいと思っても,その特徴を言語化することが難しい場合や,言語化できたとしても一般の人にとってその内容を理解できない場合などが起こりえると考えられます.我々は,絵画鑑賞中の画家の視線を実際に特殊な専用機器を用いて計測し,素人と異なる着目点およびその特徴を定量化することによって,この問題の解決を目指しています.果たして画家固有の着目点は本当に存在するのでしょうか?どのようなモデルならその着目点の特徴を適切に表現できるでしょうか?このような問いへの答えを探し求めています.また,将来的には画家特有の脳活動を捉える研究も行いたいと考えています.
動物の行動の解釈を目指した自動的定量評価
動物実験は生物学・医学・生理学・薬学など幅広い分野で実施されており, 動物の行動を観察・解析した結果が科学の発展や人類の健康・福祉の向上に大いに役立てられています. しかし, 動物の行動の観察は,未だに実験者の目や耳に頼って行われることが多い状況です.このような状況から,(1) 観察に伴う労力・時間的コストが実験者に生じること, (2) 主観的な評価が入ることによって再現性は必ずしも保証されないこと, などが問題となってきます. これら問題の解決策の一つとして, 被験動物の動画像や音声データに対して情報処理技術を適用することで行動を自動的に定量評価するような手法に期待が集まっています.実際に,数理情報学研究室ではマウスの行動を記録した動画データ,ジュウシマツの歌の音声データからそのような自動定量評価を行っています.この研究によって,これまで認識されてこなかった新たな行動の発見や,動物間のコミュニケーションの解明に繋がることを我々は期待しています.ここでは,マウスの行動解析についてもう少し深く紹介したいと思います.
マウスの行動を画像から自動的に評価しようと考えた時,幾つもの問題があることに気付かされます.(1) そもそもマウスの行動には未知のものが存在しうる,(2) 行動は全てで何種類あるのか不明である,(3) 行動を表現するには画像からどのような情報を抽出して用いるべきなのか既存の知見では十分に分かっていない,(4) 同一と考えられる行動を取っている場合でも姿勢等に様々なバリエーションがある,(5) 個体が異なれば,体型の違いが存在する,(6) 複数個体が存在する場合は一部の個体の身体部分が他個体によって隠されてしまうことがある,など枚挙に遑がありません.最初の2つの問題はノンパラメトリックベイズ法による解決を図っています.また,他の問題についても少しずつ,着実に解決して,動物行動の解釈の実現に向けて日々この研究に取り組んでいます.

おわりに
私達の研究室で行っている研究の一部をご紹介しました.それぞれ内容は異なりますが,いずれも目に見えないもの,抽象的なものを,数理的な手法で捉えようという点においては共通しています.逆に言えば,数理的な手法を上手く用いることができれば,そしてその場合のみに,様々な現象の背後に隠れた『真理』を明らかにできるようになると言えます.
これまで述べてきた内容以外にも紹介したい研究内容がたくさんありますが,ここでは筆舌し尽くせそうにありません.紹介した内容にご興味をお持ち頂き,もっと深く知りたいとお思いの方,他の紹介したい内容がどのようなものであるか気になる方,そんな方々は数理情報学研究室までぜひ御連絡を頂けたらと思います.数理情報学研究室の扉の先には,『真理』へと続くまだ見ぬ深遠な世界があなたを待っています.
